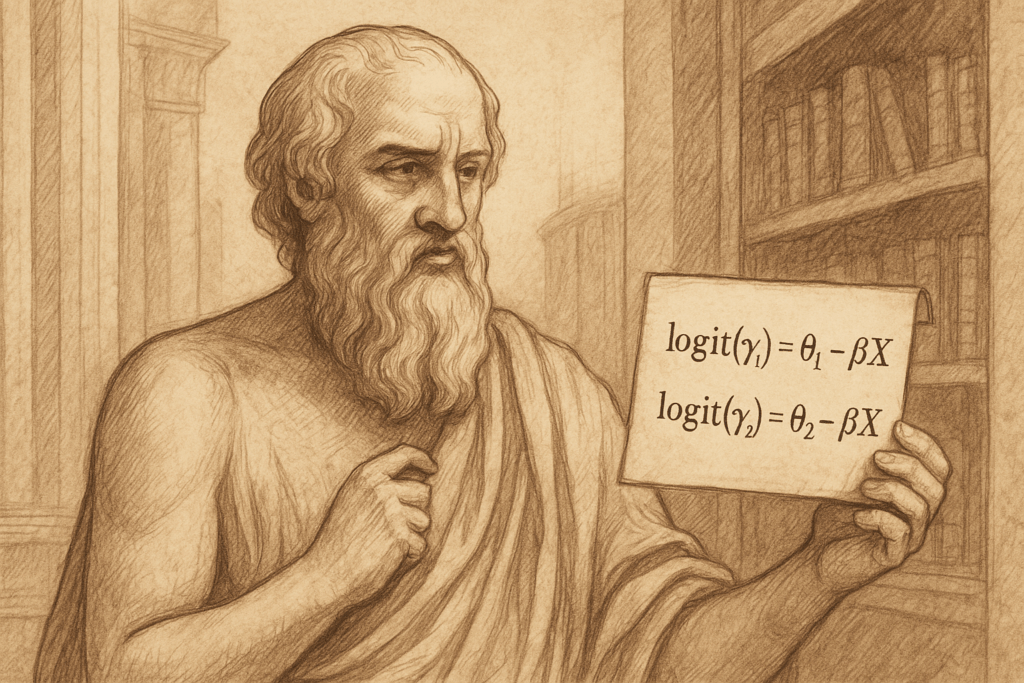You can find the full code for this example at the bottom of this post.
odds model for ordinal logistic regression was first introduced by McCullagh (1980). This model extends binary logistic regression to situations where the dependent variable is ordinal [it consists of ordered categorical values]. The proportional odds model is built on several assumptions, including independence of observations, linearity of the log-odds, absence of multicolinearity among predictors, and the proportional odds assumption. This last assumption states that the regression coefficients are constant across all thresholds of the ordinal dependent variable. Ensuring the proportional odds assumption holds is crucial for the validity and interpretability of the model.
A variety of methods have been proposed in the literature to assess model fit and, in particular, to test the proportional odds assumption. In this paper, we focus on two approaches developed by Brant in his article Brant (1990), “Assessing Proportionality in the Proportional Odds Model for Ordinal Logistic Regression.” We also demonstrate how to implement these techniques in Python, applying them to real-world data. Whether you come from a background in data science, machine learning, or statistics, this article aims to help your understand how to evaluate model fit in ordinal logistic regression.
This paper is organized into four main sections:
- The first section introduces the proportional odds model and its assumptions.
- The second section discusses how to assess the proportional odds assumption using the likelihood ratio test.
- The third section covers the assessment of the proportional odds assumption using the separate fits approach.
- The final section provides examples, illustrating the implementation of these assessment methods in Python with data.
1. Introduction to the Proportional Odds Model
Before presenting the model, we introduce the data structure. We assume we have N independent observations. Each observation is represented by a vector of p explanatory variables Xi = (Xi1, Xi2, …, Xip), along with a dependent or response variable Y that takes ordinal values from 1 to K. The proportional odds model specifically models the cumulative distribution probabilities of the response variable Y, defined as γj = P(Y ≤ j | Xi) for j = 1, 2, …, K – 1, as functions of the explanatory variables Xi. The model is formulated as follows:
logit(γⱼ) = log(γⱼ / (1 − γⱼ)) = θⱼ − βᵀ𝐗. (1)
Where θⱼ are the intercepts for each category j and respect the condition θ₁ < θ₂ < ⋯ < θₖ₋₁, and β is the vector of regression coefficients which are the same for all categories.
We observe a monotonic trend in the coefficients θⱼ across the categories of the response variable Y.
This model is also known as the grouped continuous model, as it can be derived by assuming the existence of a continuous latent variable Y∗. This latent variable follows a linear regression model with conditional mean η = βᵀ𝐗, and it relates to the observed ordinal variable Y through thresholds θⱼ defined as follows:
y∗ = βᵀ𝐗+ϵ, (2)
where ϵ is an error term (random noise), generally assumed to follow a standard logistic distribution in the proportional odds model.
The latent variable Y* is unobserved and partitioned into intervals defined by thresholds θ₁, θ₂, …, θₖ₋₁, generating the observed ordinal variable Y as follows:
In the next section, we introduce the various approaches proposed by Brant (1990) for assessing the proportional odds assumption. These methods evaluate whether the regression coefficients remain constant across the categories defined by the ordinal response variable.
2. Assessing the Proportional Odds Assumption: The Likelihood Ratio Test
To assess the proportional odds assumption in an ordinal logistic regression model, Brant (1990) proposes the use of the likelihood ratio test. This approach begins by fitting a less restrictive model in which the regression coefficients are allowed to vary across categories. This model is expressed as:
logit(γj) = θj − βjT𝐗. for j = 1, …, K-1 (4)
where βj is the vector [vector of dimension p] of regression coefficients for each category j. Here the coefficients βj are allowed to vary across categories, which means that the proportional odds assumption is not satisfied. We then use the conventionnel likelihood ratio test to assess the hypothesis :
H0 : βj = β for all j = 1, 2, …, K−1. (5)
To perform this test, we conduct a likelihood ratio test comparing the unconstrained (non-proportional or satured) model with the constrained (proportional odds or reduced) model.
Before proceeding further, we briefly recall how to use the likelihood ratio test in hypothesis testing. Suppose we want to evaluate the null hypothesis H0 : θ ∈ Θ0 against the alternative H1 : θ ∈ Θ1,
The likelihood ratio statistic is defined as:

where 𝓛(θ) is the likelihood function, θ̂ is the maximum likelihood estimate (MLE) under the full model, and θ̂₀ is the MLE under the constrained model. The test statistic λ follows a chi-square distribution with degrees of freedom equal to the difference in the number of parameters between the full and constrained models.
Here, θ̂ is the maximum likelihood estimate (MLE) under the full (unconstrained) model, and θ̂₀ is the MLE under the constrained model where the proportional odds assumption holds. The
test statistic λ follows a chi-square distribution under the null hypothesis.
In a general setting, suppose the full parameter space is denoted by
Θ = (θ₁, θ₂, …, θq, …, θp),
and the restricted parameter space under the null hypothesis is
Θ₀ = (θ₁, θ₂, …, θq).
(Note: These parameters are generic and should not be confused with the K−1 thresholds or intercepts in the proportional odds model.), the likelihood ratio test statistic λ follows a chi-square distribution with p−q degrees of freedom. Where p represents the total number of parameters in the full (unconstrained or “saturated”) model, while K−1 corresponds to the number of parameters in the reduced (restricted) model.
Now, let us apply this approach to the ordinal logistic regression model with the proportional odds assumption. Assume that our response variable has K ordered categories and that we have p predictor variables. To use the likelihood ratio test to evaluate the proportional odds assumption, we need to compare two models:
1. Unconstrained Model (non-proportional odds):
This model allows each outcome threshold to have its own set of regression coefficients, meaning that we do not assume the regression coefficients are equal across all thresholds. The model is defined as:
logit(γj) = θj − βjT𝐗. for j = 1, …, K-1 (7)
- There are K−1 threshold (intercept) parameters: θ1, θ2, … , θK-1
- Each threshold has its own vector of slope coefficients βj of dimension p
Thus, the total number of parameters in the unconstrained model is:
(K−1) thresholds + (K−1)×p slopes = (K−1)(p+1).
2. Proportional Odds Model:
This model assumes a single set of regression coefficients for all thresholds:
logit(γj) = θj − βT𝐗. for j = 1, …, K-1 (8)
- There are K−1 threshold parameters
- There is one common slope vector β (of dimension p x 1) for all j
Thus, the total number of parameters in the proportional odds model is:
(K−1) thresholds+p slopes=(K−1)+p
Thus, the likelihood ratio test statistic follows a chi-square distribution with degrees of freedom:
df = [(K−1)×(p+1)]−[(K−1)+p] = (K−2)×p
This test provides a formal way to assess whether the proportional odds assumption holds for the given data. At a significance level of 1%, 5%, or any other conventional threshold, the proportional odds assumption is rejected if the test statistic λ exceeds the critical value from the chi-square distribution with (K−2)×p degrees of freedom.
In other words, we reject the null hypothesis
H0 : β1 = β2 = ⋯ =βK-1 = β,
which states that the regression coefficients are equal across all cumulative logits. This test has the advantage of being straightforward to implement and provides an overall assessment of the proportional odds assumption.
In the next section, we introduce the proportional odds test based on separate fits.
3. Assessing the Proportional Odds Assumption: The Separate Fits Approach.
To understand this section, it’s important first to understand the concept and properties of the Mahalanobis distance. This distance is used to quantify how different two vectors are in a multivariate space that shares the same distribution.
Let x = (x₁, x₂, …, xₚ)ᵀ and y = (y₁, y₂, …, yₚ)ᵀ. The Mahalanobis distance between them is defined as:

where Σ is the covariance matrix of the distribution. The Mahalanobis distance squared is closely related to the chi-squared (χ²) distribution. Specifically, if X ∼ N(μ, Σ) is a p-dimensional normally distributed random vector with mean μ and covariance matrix Σ, then the Mahalanobis distance Dₘ(X, μ)2 follows a χ² distribution with p degrees of freedom.
Understanding this relationship is crucial for evaluating proportionality using separate model fits — a topic we will return to shortly.
In fact, the author notes that the natural approach to evaluating the proportional odds assumption is to fit a set of K−1 binary logistic regression models (where K is the number of categories of the response variable), and then use the statistical properties of the estimated parameters to construct a test statistic for the proportional odds hypothesis.
The procedure is as follows:
First, we construct separate binary logistic regression models for each threshold j = 1, 2, …, K−1 of the ordinal response variable Y. For each threshold j, we define a binary variable Zj, which takes the value 1 if the observation exceeds threshold j, and 0 otherwise. Specifically, we have:

With the probability, πj = P(Zj = 1 | X) = 1−γj satisfying the logistic regression model:
logit(πj ) = θj − βT𝐗. for j = 1, …, K-1 (10)
Then, assessing the proportional odds assumption in this context involves testing the hypothesis that the regression coefficients βj are equal across all K−1 models. This is equivalent to testing the hypothesis:
H0 : β1 = β2 = ⋯ = βK-1 (11)
Let β̂ⱼ denote the maximum likelihood estimators of the regression coefficients for each binary model, and let β̂ = (β̂₁ᵀ, β̂₂ᵀ, …, β̂ₖ₋₁ᵀ)ᵀ represent the global vector of estimators. This vector is asymptotically normally distributed, such that 𝔼(β̂ⱼ) ≈ β, with variance-covariance matrix 𝕍(β̂ⱼ). The general term of this matrix, cov(β̂ⱼ, β̂ₖ), needs to be determined and is given by:

where Cov(β̂ⱼ, β̂ₖ) is the covariance between the estimated coefficients of the j-th and k-th binary models. The asymptotic covariances, Cov(β̂ⱼ, β̂ₖ), are obtained by deleting the first row and column of:
(X+T Wjj X₊)-1X+TWjlX+ (Xᵗ WllX₊)-1
where Wjl: n × n is diagonal with typical entry πl − πj πl for j ≤ l, and X+: n x p matrix denotes the matrix of explanatory variables augmented on the left with a column of ones [1’s].
To evaluate the proportional odds assumption, Brant constructs a matrix 𝐃 that captures the differences between the coefficients β̂ⱼ. Recall that each vector β̂ⱼ has dimension p. The matrix 𝐃 is defined as follows:

where 𝐈 is the identity matrix of size p × p. The first row of the matrix 𝐃 corresponds to the difference between the first and second coefficients, the second row corresponds to the difference between the second and third coefficients, and so on, until the last row which corresponds to the difference between the (K − 2)-th and (K − 1)-th coefficients. We can notice that the product 𝐃β̂ will yield a vector of differences between the coefficients β̂ⱼ.
Once the matrix 𝐃 is constructed, Brant defines the Wald statistic X² to test the proportional odds assumption. This statistic can be interpreted as the Mahalanobis distance between the vector 𝐃β̂ and the zero vector. The Wald statistic is defined as follows:

which will be asymptotically χ² distributed with (K − 2)p degrees of freedom under the null hypothesis. The challenging part here is to determine the variance-covariance matrix 𝕍̂(β̂). In his article, Brant provides an explicit estimator for this variance-covariance matrix, which is based on the maximum likelihood estimators β̂ⱼ from each binary model.
In the following sections, we implement these approaches in Python, using the statsmodels package for the regressions and statistical tests.
Example: Application of the Two Proportional Odds Tests
The data for this example comes from the “Wine Quality” dataset, which contains information about red wine samples and their quality ratings. The dataset includes 1,599 observations and 12 variables. The target variable, “quality,” is ordinal and originally ranges from 3 to 8. To ensure enough observations in each group, we combine categories 3 and 4 into a single category (labeled 4), and categories 7 and 8 into a single category (labeled 7), so the response variable has four levels. We then handle outliers in the explanatory variables using the Interquartile Range (IQR) method. Finally, we select three predictors—volatile acidity, free sulfur dioxide, and total sulfur dioxide—to use in our ordinal logistic regression model, and we standardize these variables to have a mean of 0 and a standard deviation of 1.
Tables 1 and 2 below present the results of the three binary logistic regression models and the proportional odds model, respectively. Several discrepancies can be seen in these tables, particularly in the “volatile acidity” coefficients. For instance, the difference in the “volatile acidity” coefficient between the first and second binary models is -0.280, while the difference between the second and third models is 0.361. These differences suggest that the proportional odds assumption may not hold [I also suggest to compute standard errors of difference for more confidence].


To assess the overall significance of the proportional odds assumption, we perform the likelihood ratio test, which yields a test statistic of LR = 53.207 and a p-value of 1.066 × 10-9 when compared to the chi-square distribution with 6 degrees of freedom. This result indicates that the proportional odds assumption is violated at the 5% significance level, suggesting that the model may not be appropriate for the data. We also use the separate fits approach to further investigate this assumption. The Wald test statistic is computed as X2 = 41.880, with a p-value of 1.232 × 10-7, also based on the chi-square distribution with 6 degrees of freedom. This further confirms that the proportional odds assumption is violated at the 5% significance level.
Conclusion
This paper had two main goals: first, to illustrate how to test the proportional odds assumption in the context of ordinal logistic regression, and second, to encourage readers to explore Brant (1990)’s article for a deeper understanding of the topic.
Brant’s work extends beyond assessing the proportional odds assumption—it also provides methods for evaluating the overall adequacy of the ordinal logistic regression model. For instance, he discusses how to test whether the latent variable Y∗ truly follows a logistic distribution or whether an alternative link function might be more appropriate.
In this article, we focused on a global assessment of the proportional odds assumption, without investigating which specific coefficients may be responsible for any violations. Brant also addresses this finer-grained analysis, which is why we strongly encourage you to read his article in full.
Image Credits
All images and visualizations in this article were created by the author using Python (pandas, matplotlib, seaborn, and plotly) and excel, unless otherwise stated.
References
Brant, Rollin. 1990. “Assessing Proportionality in the Proportional Odds Model for Ordinal Logistic Regression.” Biometrics, 1171–78.
McCullagh, Peter. 1980. “Regression Models for Ordinal Data.” Journal of the Royal Statistical Society: Series B (Methodological) 42 (2): 109–27.
Wasserman, L. (2013). All of statistics: a concise course in statistical inference. Springer Science & Business Media.
Cortez, P., Cerdeira, A., Almeida, F., Matos, T., & Reis, J. (2009). Wine Quality [Dataset]. UCI Machine Learning Repository. https://doi.org/10.24432/C56S3T.
Data & Licensing
The dataset used in this article is licensed under the Creative Commons Attribution 4.0 International (CC BY 4.0) license.
It allows for use, distribution, and adaptation, even for commercial purposes, provided that appropriate credit is given.
The original dataset was published by [Name of the Author / Institution] and is available here.
Codes
Import data and the number of observations
import pandas as pd
data = pd.read_csv("winequality-red.csv", sep=";")
data.head()
# Repartition de la variable cible quality
data['quality'].value_counts(normalize=False).sort_index()
# I want to regroup modalities 3, 4 and the modalities 7 and 8
data['quality'] = data['quality'].replace({3: 4, 8: 7})
data['quality'].value_counts(normalize=False).sort_index()
print("Number of observations:", data.shape[0])Let’s handle the outliers of the predictor variables (excluding the target variable quality) using the IQR method.
def remove_outliers_iqr(df, column):
Q1 = df[column].quantile(0.25)
Q3 = df[column].quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
return df[(df[column] >= lower_bound) & (df[column] <= upper_bound)]
for col in data.columns:
if col != 'quality':
data = remove_outliers_iqr(data, col)Create a boxplot of each variable per group of quality
var_names_without_quality = [col for col in data.columns if col != 'quality']
## Create the boxplot of each variable per group of quality
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(15, 10))
for i, var in enumerate(var_names_without_quality):
plt.subplot(3, 4, i + 1)
sns.boxplot(x='quality', y=var, data=data)
plt.title(f'Boxplot of {var} by quality')
plt.xlabel('Quality')
plt.ylabel(var)
plt.tight_layout()
plt.show()Implement Ordinal regression for the odd proportionality test.
# Implement the ordered logistic regression to variables 'volatile acidity', 'free sulfur dioxide', and 'total sulfur dioxide'
from statsmodels.miscmodels.ordinal_model import OrderedModel
from sklearn.preprocessing import StandardScaler
explanatory_vars = ['volatile acidity', 'free sulfur dioxide', 'total sulfur dioxide']
# Standardize the explanatory variables
data[explanatory_vars] = StandardScaler().fit_transform(data[explanatory_vars])
def fit_ordered_logistic_regression(data, response_var, explanatory_vars):
model = OrderedModel(
data[response_var],
data[explanatory_vars],
distr='logit'
)
result = model.fit(method='bfgs', disp=False)
return result
response_var = 'quality'
result = fit_ordered_logistic_regression(data, response_var, explanatory_vars)
print(result.summary())
# Compute the log-likelihood of the model
log_reduced = result.llf
print(f"Log-likelihood of the reduced model: {log_reduced}")Compute the full multinomial model
# The likelihood ratio test
# Compute the full multinomial model
import statsmodels.api as sm
data_sm = sm.add_constant(data[explanatory_vars])
model_full = sm.MNLogit(data[response_var], data_sm)
result_full = model_full.fit(method='bfgs', disp=False)
#summary
print(result_full.summary())
# Commpute the log-likelihood of the full model
log_full = result_full.llf
print(f"Log-likelihood of the full model: {log_full}")
# Compute the likelihood ratio statistic
LR_statistic = 2 * (log_full - log_reduced)
print(f"Likelihood Ratio Statistic: {LR_statistic}")
# Compute the degrees of freedom
df1 = (num_of_thresholds - 1) * len(explanatory_vars)
df2 = result_full.df_model - OrderedModel(
data[response_var],
data[explanatory_vars],
distr='logit'
).fit().df_model
print(f"Degrees of Freedom: {df1}")
print(f"Degrees of Freedom for the full model: {df2}")
# Compute the p-value
from scipy.stats import chi2
print("The LR statistic :", LR_statistic)
p_value = chi2.sf(LR_statistic, df1)
print(f"P-value: {p_value}")
if p_value < 0.05:
print("Reject the null hypothesis: The proportional odds assumption is violated.")
else:
print("Fail to reject the null hypothesis: The proportional odds assumption holds.")The code below constructs the Wald statistic X² = (𝐃β̂)ᵀ [𝐃𝕍̂(β̂)𝐃ᵀ]⁻¹ (𝐃β̂)
K-1 Binary Logit Estimation for Proportional Odds Assumption Check
import numpy as np
import statsmodels.api as sm
import pandas as pd
def fit_binary_models(data, explanatory_vars, y):
"""
Fits a sequence of binary logistic regression models to assess the proportional odds assumption.
Parameters:
- data: Original pandas DataFrame (must include all variables)
- explanatory_vars: List of predictor variables (features)
- y: Array-like ordinal target variable (n,) — e.g., categories like 4, 5, 6, 7
Returns:
- binary_models: List of fitted binary Logit model objects (statsmodels)
- beta_hat: (K−1) × (p+1) array of estimated coefficients (including intercept)
- var_hat: List of (p+1) × (p+1) variance-covariance matrices for each model
- z_mat: DataFrame containing the binary transformed targets z_j (for inspection/debugging)
- thresholds: List of thresholds used to create the binary models
"""
qualities = np.sort(np.unique(y)) # Sorted unique categories of y
thresholds = qualities[:-1] # Thresholds to define binary models (K−1)
p = len(explanatory_vars)
n = len(y)
K_1 = len(thresholds)
binary_models = []
beta_hat = np.full((K_1, p+1), np.nan) # To store estimated coefficients
p_values_beta_hat = np.full((K_1, p+1), np.nan) # To store p-values
var_hat = []
z_mat = pd.DataFrame(index=np.arange(n)) # For storing binary target versions
X_with_const = sm.add_constant(data[explanatory_vars]) # Design matrix with intercept
# Fit one binary logistic regression for each threshold
for j, t in enumerate(thresholds):
z_j = (y > t).astype(int) # Binary target: 1 if y > t, else 0
z_mat[f'z>{t}'] = z_j
model = sm.Logit(z_j, X_with_const)
res = model.fit(disp=0)
binary_models.append(res)
beta_hat[j, :] = res.params.values # Store coefficients (with intercept)
p_values_beta_hat[j, :] = res.pvalues.values
var_hat.append(res.cov_params().values) # Store full (p+1) × (p+1) covariance matrix
return binary_models, beta_hat, X_with_const, var_hat, z_mat, thresholds
# Apply the function to the data
binary_models, beta_hat, X_with_const, var_hat, z_mat, thresholds = fit_binary_models(
data, explanatory_vars, data[response_var]
)
# Display the estimated coefficients
print("Estimated coefficients (beta_hat):")
print(beta_hat)
# Display the design matrix (predictors with intercept)
print("Design matrix X (with constant):")
print(X_with_const)
# Display the thresholds used to define the binary models
print("Thresholds:")
print(thresholds)
# Display first few rows of the binary response matrix
print("z_mat (created binary target variables):")
print(z_mat.head())
Compute Fitted Probabilities (π̂) for constructing the Wjl n x n diagonal matrix.
def compute_pi_hat(binary_models, X_with_const):
"""
Computes the fitted probabilities π̂ for each binary logistic regression model.
Parameters:
- binary_models: List of fitted Logit model results (from statsmodels)
- X_with_const : 2D array of shape (n, p+1) — the design matrix with intercept included
Returns:
- pi_hat: 2D array of shape (n, K−1) containing the predicted probabilities
from each of the K−1 binary models
"""
n = X_with_const.shape[0] # Number of observations
K_1 = len(binary_models) # Number of binary models (K−1)
pi_hat = np.full((n, K_1), np.nan) # Initialize prediction matrix
# Compute fitted probabilities for each binary model
for m, model in enumerate(binary_models):
pi_hat[:, m] = model.predict(X_with_const)
return pi_hat
# Assuming you already have:
# - binary_models: list of fitted models from previous function
# - X_with_const: design matrix with intercept (n, p+1)
pi_hat = compute_pi_hat(binary_models, X_with_const)
# Display the shape and a preview of the predicted probabilities matrix
print("Shape of pi_hat:", pi_hat.shape) # Expected shape: (n, K−1)
print("Preview of pi_hat:\n", pi_hat[:5, :]) # First 5 rows
Compute the overall estimated covariance matrix V̂(β̃) in two steps.
import numpy as np
# Assemble Global Variance-Covariance Matrix for Slope Coefficients (Excluding Intercept)
def assemble_varBeta(pi_hat, X_with_const):
"""
Constructs the global variance-covariance matrix (varBeta) for the slope coefficients
estimated from a sequence of binary logistic regressions.
Parameters:
- pi_hat : Array of shape (n, K−1), fitted probabilities for each binary model
- X_with_const : Array of shape (n, p+1), design matrix including intercept
Returns:
- varBeta : Array of shape ((K−1)*p, (K−1)*p), block matrix of variances and covariances
across binary models (intercept excluded)
"""
# Ensure input is a NumPy array
X = X_with_const.values if hasattr(X_with_const, 'values') else np.asarray(X_with_const)
n, p1 = X.shape # p1 = p + 1 (including intercept)
p = p1 - 1
K_1 = pi_hat.shape[1]
# Initialize global variance-covariance matrix
varBeta = np.zeros((K_1 * p, K_1 * p))
for j in range(K_1):
pi_j = pi_hat[:, j]
Wj = np.diag(pi_j * (1 - pi_j)) # Diagonal weight matrix for model j
XtWjX_inv = np.linalg.pinv(X.T @ Wj @ X)
# Remove intercept (exclude first row/column)
var_block_diag = XtWjX_inv[1:, 1:]
row_start = j * p
row_end = (j + 1) * p
varBeta[row_start:row_end, row_start:row_end] = var_block_diag
for l in range(j + 1, K_1):
pi_l = pi_hat[:, l]
Wml = np.diag(pi_l - pi_j * pi_l)
Wl = np.diag(pi_l * (1 - pi_l))
XtWlX_inv = np.linalg.pinv(X.T @ Wl @ X)
# Compute off-diagonal block
block_cov = (XtWjX_inv @ (X.T @ Wml @ X) @ XtWlX_inv)[1:, 1:]
col_start = l * p
col_end = (l + 1) * p
# Fill symmetric blocks
varBeta[row_start:row_end, col_start:col_end] = block_cov
varBeta[col_start:col_end, row_start:row_end] = block_cov.T
return varBeta
# Compute the global variance-covariance matrix
varBeta = assemble_varBeta(pi_hat, X_with_const)
# Display shape and preview
print("Shape of varBeta:", varBeta.shape) # Expected: ((K−1) * p, (K−1) * p)
print("Preview of varBeta:\n", varBeta[:5, :5]) # Display top-left corner
# Fill Diagonal Blocks of the Global Variance-Covariance Matrix (Excluding Intercept)
def fill_varBeta_diagonal(varBeta, var_hat):
"""
Fills the diagonal blocks of the global variance-covariance matrix varBeta using
the individual covariance matrices from each binary model (excluding intercept terms).
Parameters:
- varBeta : Global variance-covariance matrix of shape ((K−1)*p, (K−1)*p)
- var_hat : List of (p+1 × p+1) variance-covariance matrices (including intercept)
Returns:
- varBeta : Updated matrix with diagonal blocks filled (intercept removed)
"""
K_1 = len(var_hat) # Number of binary models
p = var_hat[0].shape[0] - 1 # Number of predictors (excluding intercept)
for m in range(K_1):
block = var_hat[m][1:, 1:] # Remove intercept from variance block
row_start = m * p
row_end = (m + 1) * p
varBeta[row_start:row_end, row_start:row_end] = block
return varBeta
# Flatten the slope coefficients (excluding intercept) into betaStar
betaStar = beta_hat[:, 1:].flatten()
# Fill the diagonal blocks of the global variance-covariance matrix
varBeta = fill_varBeta_diagonal(varBeta, var_hat)
# Output diagnostics
print("Shape of varBeta after diagonal fill:", varBeta.shape) # Expected: ((K−1)*p, (K−1)*p)
print("Preview of varBeta after diagonal fill:\n", varBeta[:5, :5]) # Top-left preview
Construction of the (k – 2)p x (k – I)p contrast matrix.
import numpy as np
def construct_D(K_1, p):
"""
Constructs the contrast matrix D of shape ((K−2)*p, (K−1)*p) used in the Wald test
for assessing the proportional odds assumption in ordinal logistic regression.
Parameters:
- K_1 : int — number of binary models, i.e., K−1 thresholds
- p : int — number of explanatory variables (excluding intercept)
Returns:
- D : numpy array of shape ((K−2)*p, (K−1)*p), encoding differences between
successive β_j slope vectors (excluding intercepts)
"""
D = np.zeros(((K_1 - 1) * p, K_1 * p)) # Initialize D matrix
I = np.eye(p) # Identity matrix for block insertion
# Fill each row block with I and -I at appropriate positions
for i in range(K_1 - 1): # i = 0 to (K−2)
for j in range(K_1): # j = 0 to (K−1)
if j == i:
temp = I # Positive identity block
elif j == i + 1:
temp = -I # Negative identity block
else:
temp = np.zeros((p, p)) # Zero block otherwise
row_start = i * p
row_end = (i + 1) * p
col_start = j * p
col_end = (j + 1) * p
D[row_start:row_end, col_start:col_end] += temp
return D
# Construct and inspect D
D = construct_D(len(thresholds), len(explanatory_vars))
print("Shape of D:", D.shape) # Expected: ((K−2)*p, (K−1)*p)
print("Preview of D:\n", D[:5, :5]) # Top-left corner of D
Compute the Wald Statistic for Testing the Proportional Odds Assumption
def wald_statistic(D, betaStar, varBeta):
"""
Computes the Wald chi-square statistic X² to test the proportional odds assumption.
Parameters:
- D : (K−2)p × (K−1)p matrix that encodes linear contrasts between slope coefficients
- betaStar : Flattened vector of estimated slopes (excluding intercepts), shape ((K−1)*p,)
- varBeta : Global variance-covariance matrix of shape ((K−1)*p, (K−1)*p)
Returns:
- X2 : Wald test statistic (scalar)
"""
Db = D @ betaStar # Linear contrasts of beta coefficients
V = D @ varBeta @ D.T # Variance of the contrasts
inv_V = np.linalg.inv(V) # Pseudo-inverse ensures numerical stability
X2 = float(Db.T @ inv_V @ Db) # Wald statistic
return X2
# Assumptions:
K_1 = len(binary_models) # Number of binary models (K−1)
p = len(explanatory_vars) # Number of explanatory variables (excluding intercept)
# Construct contrast matrix D
D = construct_D(K_1, p)
# Compute the Wald statistic
X2 = wald_statistic(D, betaStar, varBeta)
# Degrees of freedom: (K−2) × p
ddl = (K_1 - 1) * p
# Compute the p-value from the chi-square distribution
from scipy.stats import chi2
pval = 1 - chi2.cdf(X2, ddl)
# Output results
print(f"Wald statistic X² = {X2:.4f}")
print(f"Degrees of freedom = {ddl}")
print(f"p-value = {pval:.4g}")